CSP201412-2_by_C

问题描述

试题编号：201412-2

试题名称：Z字形扫描

时间限制：2.0s

内存限制：256.0MB

问题描述

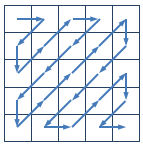
　在图像编码的算法中，需要将一个给定的方形矩阵进行Z字形扫描(Zigzag Scan)。给定一个n×n的矩阵，Z字形扫描的过程如下图所示：

​

　对于下面的4×4的矩阵，

　1 5 3 9

　3 7 5 6

　9 4 6 4

　7 3 1 3

　对其进行Z字形扫描后得到长度为16的序列：

　1 5 3 9 7 3 9 5 4 7 3 6 6 4 1 3

　请实现一个Z字形扫描的程序，给定一个n×n的矩阵，输出对这个矩阵进行Z字形扫描的结果。

输入格式

　输入的第一行包含一个整数n，表示矩阵的大小。

　输入的第二行到第n+1行每行包含n个正整数，由空格分隔，表示给定的矩阵。

输出格式

　输出一行，包含n×n个整数，由空格分隔，表示输入的矩阵经过Z字形扫描后的结果。

样例输入

4
1 5 3 9
3 7 5 6
9 4 6 4
7 3 1 3

样例输出

1 5 3 9 7 3 9 5 4 7 3 6 6 4 1 3

评测用例规模与约定

　1≤n≤500，矩阵元素为不超过1000的正整数。

代码

>#include<stdio.h>

>int main()
>{
int arr[50][50];
int arr2[2500];
int n = 0;
int i = 0;
scanf("%d", &n);
for (i = 0; i < n; i++)
{
	int k = 0;
	for(k = 0; k < n; k++)
	{
		scanf("%d", &arr[i][k]);
	}
}

int row = 0, col = 0;
arr2[0] = arr[row][col];
for (i = 0; i < n*n-1; i)
{
	if (col == 0&&row != n-1)
	{
		row++;//到头先往下走一格
		i++;
		arr2[i] = arr[row][col];
		
		int k = 0;
		int mid = row - col;
		for (k = 0; k < mid; k++)
		{
			col++;
			row--;
			i++;
			arr2[i] = arr[row][col];//往上数
		}
	}
	
	if (row == 0&&col != n-1) 
	{
		i++;
		col++;//到头先往右走一格
		arr2[i] = arr[row][col];
		int j = 0;
		int mid = col - row;
		for (j = 0; j < mid; j++)
		{
			i++;
			col--;
			row++;
			arr2[i] = arr[row][col];//往下数
		}
	}
	if (col == n - 1)
	{ 
		row++;
		i++;
		arr2[i] = arr[row][col];
		int j = 0;
		int mid = col - row;
		if (col == n - 1 && row == n - 1)
			break;
		for (j = 0; j < mid; j++)
		{
			col--;
			row++;
			i++;
			arr2[i] = arr[row][col];//往下数
		}
	}
	if (row == n - 1&&col != n-1)
	{
		col++;
		i++;
		arr2[i] = arr[row][col];
		int k = 0;
		int mid = row - col;
		for(k = 0; k < mid; k++)
		{
			col++;
			row--;
			i++;
			arr2[i] = arr[row][col];//往上数
		}

	}

}
int m = 0;
printf("\n");
for(m = 0; m < n*n; m++)
{
	printf("%d ", arr2[m]);
}

>}

方法实现

1. 使用一个二维数组储存输入的数字方阵,另一个数组来储存一维化后的数组
2. 使用for语句进行循环,当遍历完成后退出
3. row与col来记录当前所处的行与列,if语句进行判断
4. 当满足条件后使用对应的方法进行遍历(往上数/往下数)
5. 满足条件跳出循环,打印数组